This is a 4-week course on different families of mathematical modelling techniques, ranging from statistical modelling to Ordinary differential equations, from analytical to numerical techniques of solution.
We began with systems analysis on sets of differential equations. It always amazes me as an engineer, who loves using numerical solvers to compute and visualise systems behaviour, to see that using analytical techniques, one can tell the characteristics of the system behaviour in a quantifiable way. It does require a reasonable amount of algebraic manipulations, which haunted some colleagues who were not from a numerical background. It nevertheless introduces me to the ground work that mathematicians have done – from which engineers have taken for application into real world problems.
Then we had some lectures on numerical techniques for solving ODEs and PDEs. Admittedly in order to tailor the course to fit with everyone’s appetite, a lot of the interesting contents had been shrunk down to actual mathematical proof – it was fine to me coming from an engineering background because I can relate to the actual scenarios where numerical instability happens ; however I doubt if the chemists and biologists among us would ever interpret… this was brighten up though, by the M&M picking exercise simulating the prey-predator relationship (a classical mathematical model!). It was a fun afternoon to play around with data collection and model fitting to see the hiccups of mathematical modelling – there were huge discrepancies between the model parameters proposed by different groups based on their data, among which were unreliable parameters (e.g. Negative values for “death rate” etc.).
We also had some stochastic modelling based on the Gillespie algorithm. Apparently Monte Carlo is a very versatile technique that has been used everywhere in Systems Biology. Gillespie algorithm operates on a system of reactions. It randomises the time step taken for a reaction to occur. The probability that a certain reaction is chosen to occur at each time-step depends on the quantity of reactant molecules existing in th system at the time. This was my first encounter with stochastic modelling.
Following this we have some statistics lectures on graph theories, in particular on protein interaction networks. Some of the labour-intensive work had been compiled to run in R, but learning the theories behind network topological features and how one could interpret by looking at a network presented another approach to Systems biology research: how can we interrupt protein interactions in order to suppress disease progression?
Finally we had lectures on Bayesian inference. Perhaps this was the third time when we had specific lectures on Bayesian inference – therefore, together with the lecturer’s very funny examples, Bayesian inference becomes a theory that is a lot easier to understand and apply. This is particularly useful for biological applications which require the “ambiguities” accounted for in Bayesian statistics.
Obviously, squeezing a third year maths curriculum into a 4-week course is, indeed, very intense, yet many of us found it an enjoyable module relating our background to actual applications on biological research.
We summed up the module by presenting a mathematical biology paper. Our group selected a network analysis paper based on herpesvirus evolution and their conservatory protein interactions. Despite being a rather primitive research paper (they have obviously introduced some very critical ideas, but the evidence on the conservation of core protein interactions was rather flaky!), we had fun running some network topological studies, reproducing some of their graphs using the currently updated knowledge of orthologous proteins.
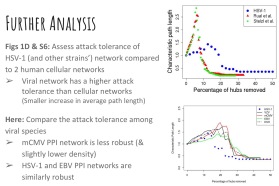
Fig. 1. Playing around with network analysis (Attack Tolerance assessed for increase in average path length upon progressive removal of highest-degree node)
Not long to go before our first rotation project! Bashing through this half-a-year of training is actually demanding, but fruitful, and full of adventures!